Đánh giá hệ thống Information Retrieval (tiếp theo)

Tiếp theo về các chỉ số đánh giá các hệ thống Information Retrieval, bài này sẽ bàn về đánh giá hệ thống tìm kiếm với Ground truth là non-binary (không phải nhị phân) và đánh giá hệ thống large scale.

Với các bộ Ground truth không phải là nhị phân, ta không thể sử dụng các độ đo như Precision, Recall, ..., ta dùng một số độ đo khác. Tương tự, với hệ thống ở mức độ cực lớn, ta không thể nào tính được recall, do chỉ biết được kết quả trả về ở những trang đầu.

Information Retrieval

Chỉ số đánh giá khi Ground truth là non-binary

a. Precision & Recall

Precision & Recall là 2 độ đo phổ biến, nhất là trong các hệ thống phân lớp (binary classification), information retrieval, ...

  • Precision: độ chính xác, ví dụ hệ thống tìm kiếm trả về 30 kết quả, trong đó

$$ {\displaystyle {\text{precision}}={\frac {{{\text{Tổng số kết quả trả về đúng}}}}{|{{\text{Tổng số kết quả trả về}}}|}}} $$

  • Recall: độ phủ

$$ {\displaystyle {\text{precision}}={\frac {{{\text{Tổng số kết quả trả về đúng}}}}{|{{\text{Tổng số kết quả đúng}}}|}}} $$

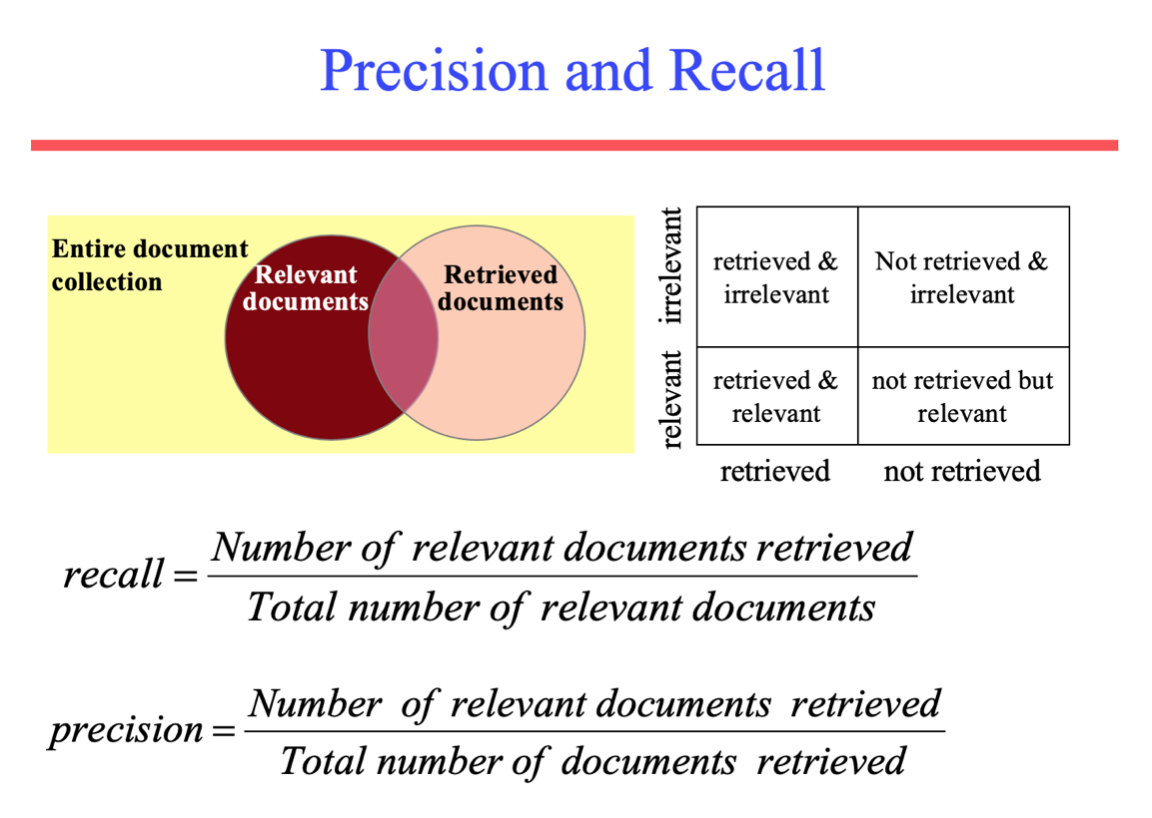
Trade off

Ví dụ, hệ thống tìm kiếm cho kết quả 30 trang, trong đó có 20 trang đúng. Nhưng thực sự trong toàn bộ hệ thống sẽ có tất cả 40 trang đúng. Vậy precision sẽ là 20/30 = 2/3, recall là 20/40 = 1/2.

Tham khảo thêm:

Một hệ thống tốt sẽ có sự đánh đổi giữa Precision và Recall. Thực tế cho rằng: Precision giảm khi recall tăng

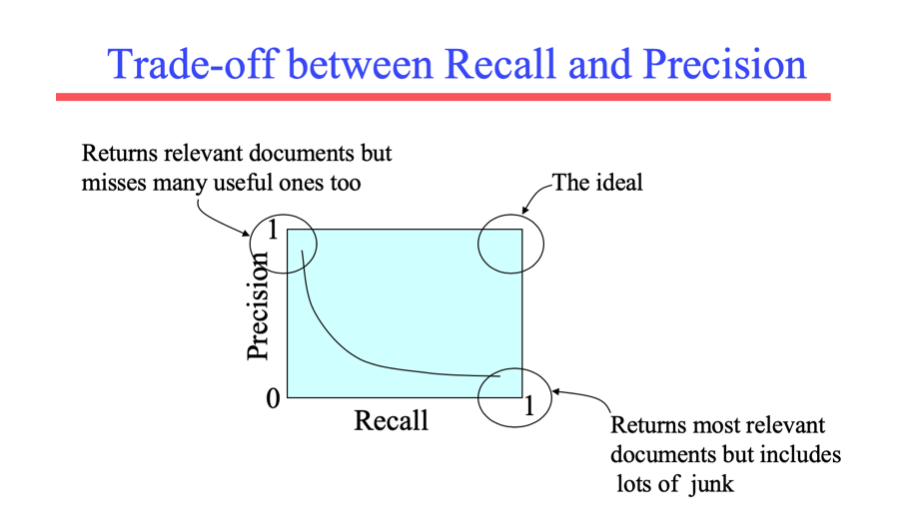
Trade off

  • Bạn có thể tăng recall bằng cách tăng số docs trả về.
  • Recall là một hàm không tăng
  • Một hệ thống tìm kiếm trả về toàn bộ docs đạt 100% recall

b. AUC

Để đánh giá hệ thống tốt khi đánh đổi giữa Precision và Recall, ta dùng một chỉ số là AUC (Area under Curve): diện tích dưới đường vẽ của Recall-Precision.

Các vẽ đường precision-recall curve:

  • Cho một query, chọn ra top n kết quả đúng -> với mỗi n ta có một cặp recall/precision
  • Thay đổi n ta có một dãy n cặp điểm như thế.
  • Vẽ các cặp điểm này ta được đồ thị như sau:

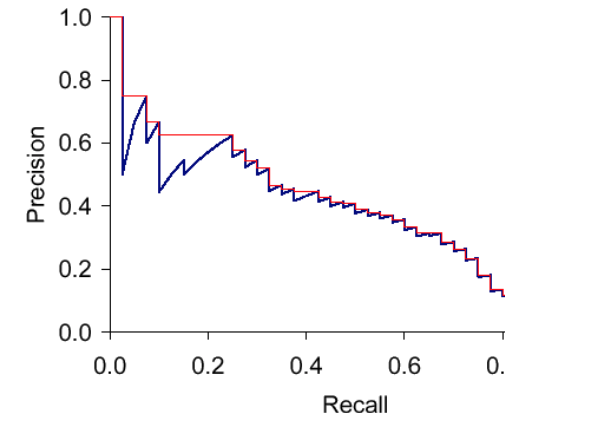
precision-recall curve

Một số điểm đồ thị sẽ bị răng cưa như trên, ta sẽ dùng kỹ thuật interpolated curve, nối các điểm như đường màu đỏ dưới đây $P(r) = \text{max}_{r' > r} P(r')$

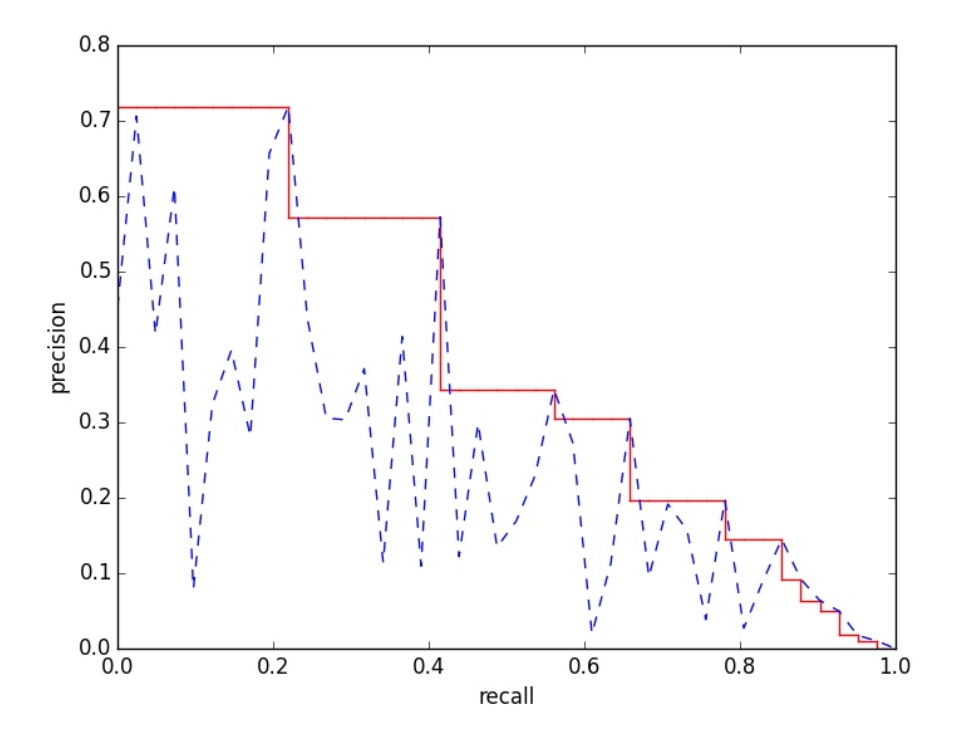
precision-recall curve

11-point interpolated average precision: tính precision trung bình ở 11 điểm

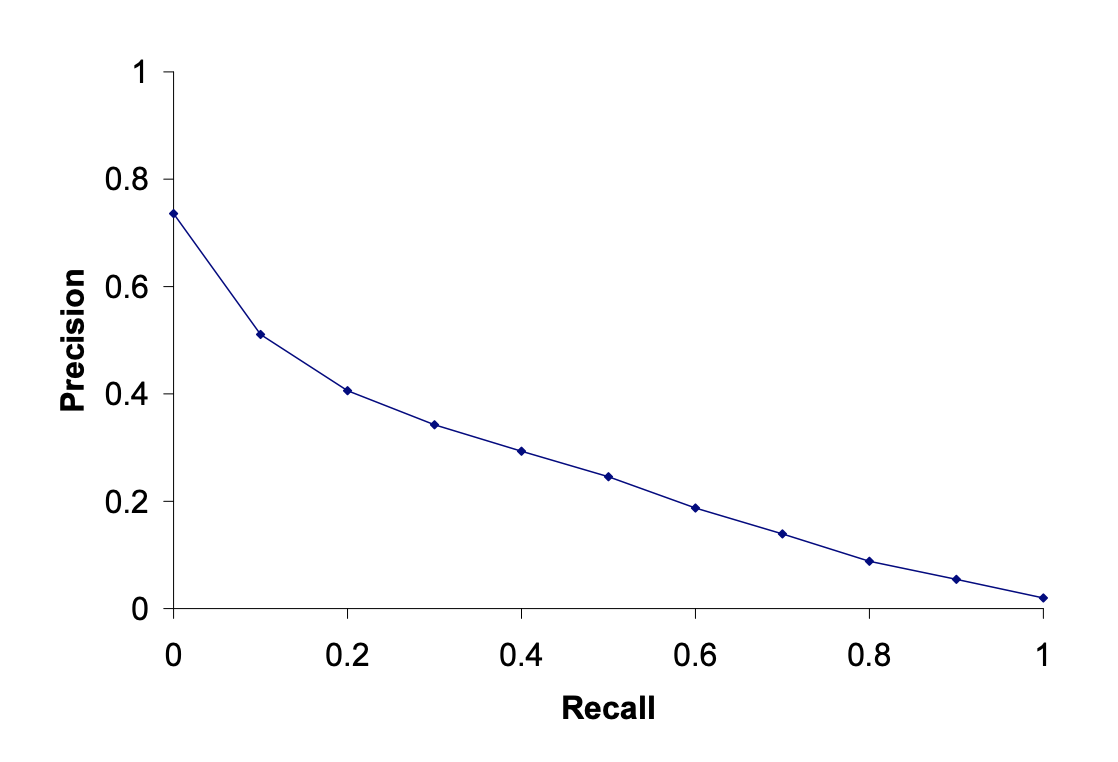
precision-recall curve

Ta tính diện tích dưới đường precision-recall curve, diện tích lớn hơn thì cho kết quả tốt hơn.

c. R-precision

Tính precision tại vị trí thứ R-th mà câu query trả về R câu trả lời.

R-precision

d. F-Measure

F-Measure ($F_1$ Score) là độ đo bao gồm vừa Precison và Recall, công thức truyền thống F-Measure là harmonic mean của precision và recall.

$$ {\displaystyle F_{1}=\left({\frac {2}{\mathrm {recall} ^{-1}+\mathrm {precision} ^{-1}}}\right)=2\cdot {\frac {\mathrm {precision} \cdot \mathrm {recall} }{\mathrm {precision} +\mathrm {recall} }}}. $$

Theo ý nghĩa toán học, để đạt được F-measure cao, ta cần Precision lẫn Recall đều cao.

e. E-Measure (parameterized F Measure)

Vẫn là F-measure nhưng có thêm tham số hiệu chỉnh, vì đôi khi ta cần Precision quan trọng hơn hoặc ngược lại.

$$ F_\beta = \frac{(1 + \beta^2) \cdot (\mathrm{precision} \cdot \mathrm{recall})}{(\beta^2 \cdot \mathrm{precision} + \mathrm{recall})}, $$

Khi đó $\beta$ sẽ điều chỉnh trọng số giữa precision và recall:

  • $\beta$ = 1: Trọng số precision và recall bằng nhau (E=F).
  • $\beta$ > 1: Trọng số recall cao hơn.
  • $\beta$ < 1: Trọng số precision cao hơn.

f. MAP (Mean Average Precision)

Đây là độ đo tổng hợp kết quả của nhiều query, được sử dụng rất phổ biến. MAP cũng chứa thông tin của precision và recall, có xét đến độ quan trọng của thứ hạng kết quả.

  • Average Precision: trung bình của các precision tại các điểm mà mỗi kết quả đúng trả về.
  • Mean Average Precision: trung bình của các Average Precision cho một tập các queries.

Tham khảo

Many slides in this post are adapted from Prof. Joydeep Ghosh (UT ECE) who in turn adapted them from Prof. Dik Lee (Univ. of Science and Tech, Hong Kong)

•Data Engineer•Data, Data Engineer, Information Retrieval, NLP•